Опытное преподавание

При доставке груза из пункта А расходы равны m+10s1. При доставке груза из пункта В расходы равны m+20s2. Если для пункта Р выгоднее доставлять груз с предприятия А, то m+10s1< m+20s2, откуда s1<2s2, в обратном случае получим s1>2s2.

Таким образом, границей области для каждой точки, до которой расходы на перевозку груза из пунктов А и В равны, будет множество точек плоскости, удовлетворяющих уравнению

s1=2s2 (1)

Выразим s1 и 2s2 через координаты:

, .

Имея в виду (1), получим .

Это и есть уравнение окружности. Следовательно, для всех пунктов, попадающих во внутреннюю область круга, выгоднее привозить груз из пункта В, а для всех пунктов, попадающих во внешнюю часть круга, - из пункта А.

Задача 2. На плоскости даны точки А и В; найти геометрическое место точек М, удаленных от А в двое больше, чем от В.

Решение:

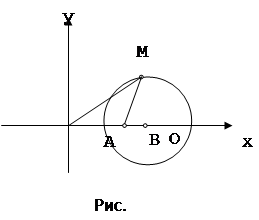Выберем систему координат на плоскости так, чтобы начало координат попало в точку А, а положительная полуось абсцисс пошла по АВ. За единицу масштаба возьмем отрезок АВ. Точка А будет иметь координаты (0,0), точка В координаты (1,0). Координаты точки М обозначим через (х,у). Условие записывается в координатах так:

.

Мы получили уравнение искомого геометрического места точек. Чтобы понять, какое множество описывается этим уравнением, мы преобразуем его так, чтобы оно приняло знакомый нам вид. Возведя обе засти в квадрат, раскрывая скобки и приводя подобные члены, получаем равенство: Зх2-8х+4+Зу2=0.

Это равенство можно переписать так:

или так: . Это уравнение окружности с центром в точке (,0) и радиусом, равным . Это значит, что наше геометрическое место точек является окружностью.

Задача 3.Дан треугольник ABC; найти центр окружности, описанной около этого треугольника.

Решение:

Примем точку А за начало координат, ось абсцисс направим от А к В. Тогда точка В будет иметь координаты (с,0), где с - длинна отрезка АВ. Пусть точка С имеет координаты (q,h), а центр искомой окружности - (а,b). Радиус этой окружности обозначим через R. Запишем в координатах принадлежность точек А(0,0), В(с,0) и C(q,h) искомой окружности:

a2+b2=R2,

(c-a)2+b2=R2,

(q-a)2+(h-b)2=R2.

Каждое из этих условий выражает тот факт, что расстояние точек А(0,0), В(с,0), C(q,h) от центра окружности (а,b) равно радиусу. Эти условия легко получить, если записать уравнение искомой окружности (окружности с центром (а,b) и радиусом R), т. е. (x-a)2+(y-b)2=R2, а затем в это уравнение вместо х и у подставить координаты точек А, В и С, лежащих на этой окружности. Эта система трех уравнений с тремя неизвестными легко решается, и мы получаем:

, ,

.

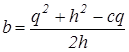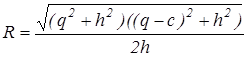Задача решена, так как мы нашли координаты центра и радиус. Причем следует заметить, что мы при решении задачи не прибегали к построению чертежа.

Домашнее задание:

Лестница, стоящая на гладком полу у стены соскальзывает вниз. По какой линии движется котенок, сидящий на середине лестницы?

В квадрат вписана окружность. Доказать, что сумма квадратов расстояний любой точки окружности до сторон квадрата постоянна.

Краткий анализ проведенных занятий: Учащиеся на уроках активно принимали участие, особенно на первом при выводе формул, так как материал не сложный и использует факты и понятия, которые были изучены не так давно и повторены на устном счете. Также на 1 уроке удалось прорешать все запланированные задачи на закрепление, особую трудность вызвала задача № 3, в которой учащиеся долго не могли сделать чертеж и путались в формулах нахождения длины и координат вектора. Проведенная на следующем уроке самостоятельная работа показала, что практически все ученики усвоили материал (с работой не справились 2 человека из 26 учеников этого класса). Наибольшее количество ошибок было сделано в задаче № 2, при использовании формулы нахождения расстояния между 2 точками. Таким образом, можно предположить, что тема «Простейшие задачи в координатах» была успешно усвоена большинством учеников данного класса.