Опытное преподавание

Опытное преподавание проводилось в 9 классе средней общеобразовательной школы №51. Перед его проведением была изучена математическая и методическая литература и разработана методика проведения факультатива. Было проведено 2 занятия. В данном классе изучение геометрии ведется по учебнику [2], поэтому в качестве основного теоретического и практического источника я выбрала данный методический комплект.

I. Занятия проводились по теме «Простейшие задачи в координатах», до ознакомления с которыми учащиеся изучали тему «Векторы», познакомились с понятием «координаты вектора», а также узнали формулу середины отрезка.

1 занятие: «Простейшие задачи в координатах»

Образовательная цель урока – рассмотреть задачи о вычислении длины вектора по его координатам и по координатам его начала и конца; показать, как они используются при решении других задач.

Содержание урока:

Вначале урока был проведен устный счет для проверки усвоения материала, разобранного на прошлом уроке, а также для проведения пропедевтической работы по повторению тех понятий и фактов, которые будут использованы при объяснении нового материала.

Устный счет:

Координаты точек А(-2, 3) и В(2, -4). Найдите координаты векторов и .

Координаты точек М(5,-8) и Р(-3, 4). Найдите координаты точки О (О – середина отрезка МР).

СР – диагональ окружности; С(-2, -1), Р(5, 7). Найдите координаты центра окружности – точки Е.

ABCD – прямоугольник, АD=7, АВ=5. Найдите АС.

Новый материал:

Вычисление длины вектора по его координатам.

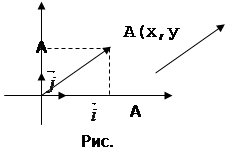
Вывод формулы опирается на теорему Пифагора и на то, что расстояние между двумя точками оси координат находится по формулам (для точек ; оси х) и (для точек ; оси у). Покажем, что длина вектора равна . Данная формула доказывается только для случая, когда х≠0 и у≠0, в достоверности других случаев учащимся предоставляется убедиться самостоятельно. Для доказательства задаем координатную плоскость и рассматриваем вектор с началом в начале координат (по теореме: от любой точки можно отложить вектор, равный данному и притом единственный). Используя формулу для нахождения координат вектора по координатам его начала и конца, можем найти координаты точки А. Далее с помощью теоремы Пифагора находим длину отрезка ОА=. следовательно, их длины раны, т.о. .

Далее показывается применение данной формулы.

Расстояние между двумя точками.

Нахождение данной формулы опирается на использование предыдущей. Пусть имеются точки М1(х1,у1)и М2(х2,у2), необходимо найти расстояние между этими точками. Рассмотрим вектор М1М2. Его координаты равны . Находим длину вектора по его координатам: , а расстояние между М1 и М2 это длина вектора . После выведения данной формулы можно записать формулу и показать, что они эквивалентны.

Закрепление: для закрепления используется ряд задач на применение данных формул.

Найдите длины векторов: а) ; b) [2: № 938]

Найдите медиану АМ треугольника АВС, вершины которого имеют координаты: А(0,1), В(1, -4), С(5,2). [2: № 942]